3242. Design Neighbor Sum Service using Rust

Problem

ou are given a n x n 2D array grid containing distinct elements in the range [0, n2 - 1].

Implement the NeighborSum class:

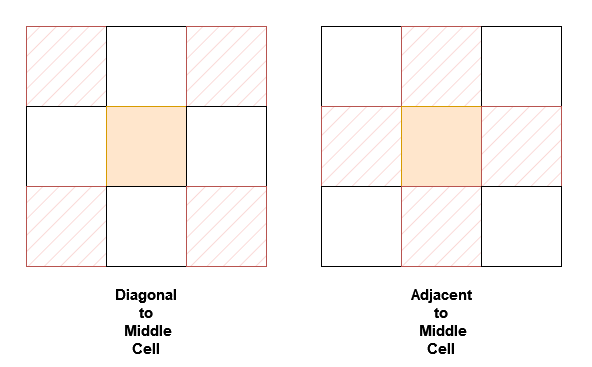
• NeighborSum(int [][]grid) initializes the object.
• int adjacentSum(int value) returns the sum of elements which are adjacent neighbors of value, that is either to the top, left, right, or bottom of value in grid.
• int diagonalSum(int value) returns the sum of elements which are diagonal neighbors of value, that is either to the top-left, top-right, bottom-left, or bottom-right of value in grid.

Example 1:

Input:

[“NeighborSum”, “adjacentSum”, “adjacentSum”, “diagonalSum”, “diagonalSum”]

[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]

Output: [null, 6, 16, 16, 4]

Explanation:

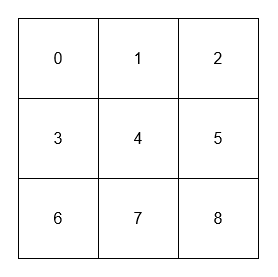
• The adjacent neighbors of 1 are 0, 2, and 4.
• The adjacent neighbors of 4 are 1, 3, 5, and 7.
• The diagonal neighbors of 4 are 0, 2, 6, and 8.
• The diagonal neighbor of 8 is 4.

Example 2:

Input:

[“NeighborSum”, “adjacentSum”, “diagonalSum”]

[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]

Output: [null, 23, 45]

Explanation:

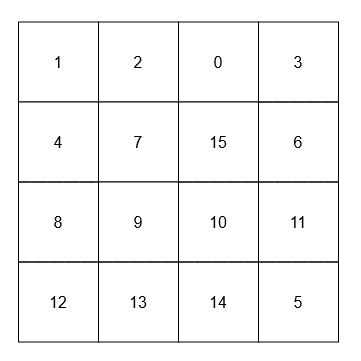
• The adjacent neighbors of 15 are 0, 10, 7, and 6.
• The diagonal neighbors of 9 are 4, 12, 14, and 15.

Constraints:

• 3 <= n == grid.length == grid[0].length <= 10
• 0 <= grid[i][j] <= n2 - 1
• All grid[i][j] are distinct.
• value in adjacentSum and diagonalSum will be in the range [0, n2 - 1].
• At most 2 * n2 calls will be made to adjacentSum and diagonalSum.

Solution

First attempt : Time complexity O(n2)

struct NeighborSum {
 grid:Vec<Vec<i32>>
}


/** 
 * `&self` means the method takes an immutable reference.
 * If you need a mutable reference, change it to `&mut self` instead.
 */
impl NeighborSum {

    fn new(grid: Vec<Vec<i32>>) -> Self {
        
      //  println!("Grid {:?}", &grid);
        let inst = NeighborSum {grid};
        inst
    }
    
   fn adjacent_sum(&mut self, value: i32) -> i32 {
        //println!("Ad value {} and self is {:?}", value, self.grid);
        let mut output: i32 = 0;
        let mut getindexofvalue: i32 = 0;
        let mut vcount: i32  = 0;
        
        for itemv in &self.grid{
            let mut hcount: i32 = 0;
            for item in itemv{
                
                if(*item == value){
                  //  println!("Found value {} == {} at column {}: row {}",item,value,vcount,hcount );
                    // letc calculate neighbours now
                    let mut leftitempointer:i32 =  vcount - 1;
                    let mut rightitempointer:i32 =  vcount + 1;
                    let mut topitempointer:i32 =  hcount - 1;
                    let mut bottomitempointer :i32 =  hcount + 1;
                    let mut leftitem :i32 = 0;
                    let mut rightitem :i32 = 0;
                    let mut topitem :i32 = 0;
                    let mut bottomitem :i32 = 0;
                    if(leftitempointer >= 0){
                       // println!(" left item hcount and leftitempointer are {} : {}",hcount,leftitempointer);
                        leftitem = self.grid[leftitempointer as usize][hcount as usize];
                    }
                    if(rightitempointer < itemv.len() as i32){
                       // println!(" right item hcount and rightitempointer are {} : {}",hcount,rightitempointer);
                        rightitem = self.grid[rightitempointer as usize][hcount as usize];
                    }
                    if(topitempointer >= 0){
                       // println!(" top item topitempointer and vcount are {} : {}",topitempointer,vcount);
                        topitem = self.grid[vcount as usize][topitempointer as usize];
                    }
                    if(bottomitempointer < self.grid.len() as i32){
                       // println!(" bottom item bottomitempointer and vcount are {} : {}",bottomitempointer,vcount);
                        bottomitem = self.grid[vcount as usize][bottomitempointer as usize];
                    }
                    output = leftitem + rightitem + topitem + bottomitem;
                   // println!("Output is {} {} {} {} {}", output, leftitem, rightitem, topitem, bottomitem);
                }
                hcount = hcount + 1;
            }
            vcount = vcount +1;
           // println!("Adjecent value {} : {:?} : {:?}", value, itemv, self.grid);
        } 
       // self.grid[0][0] = 3;
       // println!("Ad value {} and self is {:?}", value, self.grid);
        return(output)
    }
    
    fn diagonal_sum(&self, value: i32) -> i32 {
    let mut output: i32 = 0;
    let mut vcount: i32 = 0;

    for itemv in &self.grid {
        let mut hcount: i32 = 0;
        for item in itemv {
            if *item == value {
                let top_left = if vcount > 0 && hcount > 0 {
                    self.grid[(vcount - 1) as usize][(hcount - 1) as usize]
                } else {
                    0
                };

                let top_right = if vcount > 0 && hcount < (itemv.len() as i32 - 1) {
                    self.grid[(vcount - 1) as usize][(hcount + 1) as usize]
                } else {
                    0
                };

                let bottom_left = if vcount < (self.grid.len() as i32 - 1) && hcount > 0 {
                    self.grid[(vcount + 1) as usize][(hcount - 1) as usize]
                } else {
                    0
                };

                let bottom_right = if vcount < (self.grid.len() as i32 - 1) && hcount < (itemv.len() as i32 - 1) {
                    self.grid[(vcount + 1) as usize][(hcount + 1) as usize]
                } else {
                    0
                };

                output = top_left + top_right + bottom_left + bottom_right;
            }
            hcount += 1;
        }
        vcount += 1;
    }

    output
}

}

/**
 * Your NeighborSum object will be instantiated and called as such:
 * let obj = NeighborSum::new(grid);
 * let ret_1: i32 = obj.adjacent_sum(value);
 * let ret_2: i32 = obj.diagonal_sum(value);
 */